高中导数基本初等函数公式全解析：初学者必学，巧记方法助力进阶

高中导数运算中，在理解概念后，基本的初等函数的导数公式可是必须要好好掌握的内容呀！否则高中阶段后续的数学学习寸步难行，记忆这些公式还是有巧妙方法的了。

（如果不理解导数概念可以看下 高中数学导数：从难以接受到豁然开朗，通俗剖析，助力深度理解）

常见基本初等函数的导数公式可以分为5大类，大概如下：

1.常数函数 的导数公式

像常数函数若

，它的导数为0。想想看，常数就像一个静止的量，没有变化趋势，比如函数y = 5，不管x咋变，y始终是5，没变化，那导数自然就是0啦。

2.幂函数 的导数公式

幂函数的导数公式(xⁿ)' = nxⁿ⁻¹也很关键。举例来说吧，函数y = x² ，按导数计算公式，它的导数就是2x 。其实就是把原来的指数拿下来当系数，指数再减1 。那y = x³ 的导数就是3x² 。大家不妨试试算下y = x⁴ 的导数。

3.指数函数的导数公式

指数函数y = aˣ （a > 0且a≠1），导数是y' = aˣlna 。特别注意的，当a = e时，y = eˣ ，它的导数就是它本身eˣ ，是不是很神奇 大家可以算算y = 2ˣ 的导数哦。

（e是什么？e是一个重要的数学常数，它是自然对数的底数，约等于2.71828。e有很多奇妙的性质和应用哦。从数学定义上来说，它可以通过极限的形式来表示，即

。其实，在很多实际问题中，比如在研究连续复利、放射性衰变、生物种群增长等自然现象和经济问题时，e都起着非常重要的作用。函数

的导数还是它本身这个性质，在高中阶段记住，直接运用就可以了啦！）

4.对数函数 的导数公式

对数函数

（a > 0且a≠1）的导数是

。需要特别注意的是当a = e时，f(x) = lnx ，导数就是1/x 。比如求y = ln2x 的导数，要用到复合函数求导法则，先记住lnx导数是1/x这个基础哦。

y = ln2x 的导数推理过程

5.三角函数 的导数公式

三角函数的导数也不能忽视。正弦函数y = sinx ，导数是y' = cosx ；余弦函数y = cosx ，导数是y' = -sinx 。其实，联想下它们的图像，能帮助我们记忆呢。

首先呢，咱们画出正弦函数y = sin x和余弦函数y = cos x的图像。正弦函数的图像就像波浪一样，在(x = 0)的时候，它是处于上升趋势的，对吧？这时候它的切线斜率是正的，而此时余弦函数

y=cos x在x = 0处的值cos0 = 1是正的。

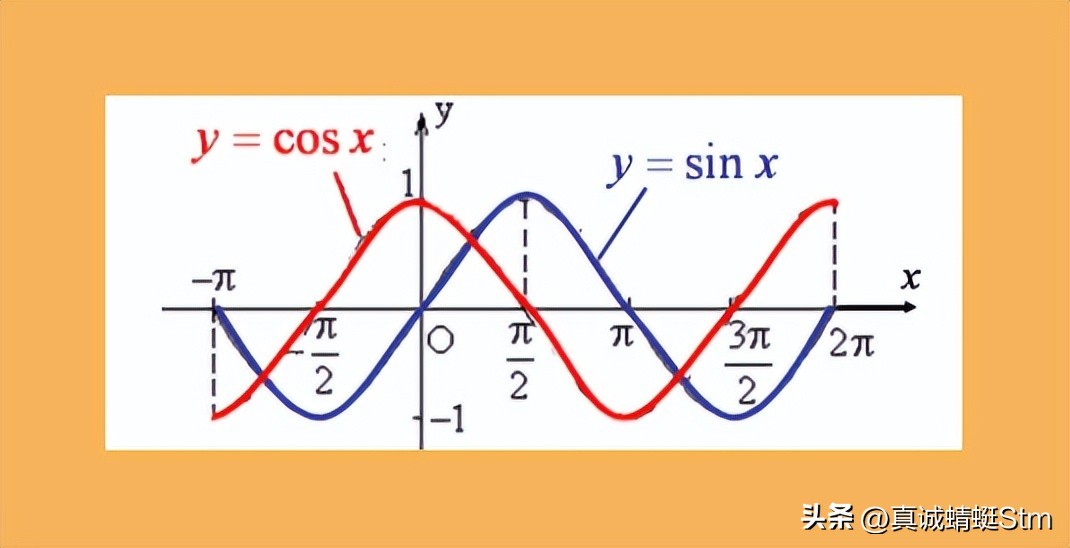
正弦函数y=sin x 余弦函数y = cos x

随着(x)的增大，当正弦函数(y=sin x)到达波峰，也就是

的时候，它在这一点的切线斜率为0)，而此时余弦函数y = cos x在

处的值为0。

再继续看，正弦函数过了波峰开始下降，在(x=π)的时候，它的切线斜率是负的，而此时余弦函数y=cos x在此处的值也是负的。

从正弦函数(y=sin x)整个图像上看，它在各个点处切线斜率的变化趋势和余弦函数y=cos x的值的变化是对应的，所以我们就可以联想记忆正弦函数的导数是余弦函数，即(sin x)'=cos x。

那对于余弦函数y=cos x呢，同样看它的图像。它在x = 0的时候，是处于水平状态然后开始下降的，切线斜率是0然后变为负的，而此时正弦函数y=sin x在x = 0处的值 0，随着x增大，它的切线斜率的变化趋势和正弦函数y = sin x的值的变化是对应的，只不过是相反的关系，所以余弦函数的导数是负的正弦函数，即(cos x)'=-sin x。

要快速记住以上这些基本初等函数的导数公式，一方面要理解推导过程，另一方面得多做练习题，通过运用加深记忆。实在理解不了，那就记住直接拿来运用也是一个策略。